Spectral phase interferometry for direct electric-field reconstruction
In ultrafast optics, spectral phase interferometry for direct electric-field reconstruction (SPIDER) is an ultrashort pulse measurement technique.
Contents |
The basics
SPIDER is an interferometric ultrashort pulse measurement technique in the frequency domain based on spectral shearing interferometry. Spectral shearing interferometry is similar in concept to lateral shearing interferometry, except the shearing is performed in the frequency domain. The spectral shear is typically generated by sum-frequency mixing the test pulse with two different quasi-monochromatic frequencies (usually derived by chirping a copy of the pulse itself). The interference between the two upconverted pulses allows the spectral phase at one frequency to be referenced to the spectral phase at a different frequency, separated by the spectral shear - the difference in frequency of the two monochromatic beams. In order to extract the phase information, a carrier fringe pattern is introduced, typically by delaying the two spectrally sheared copies with respect to one another.
Theory
There are two important specifications for filters: time/frequency response and amplitude/phase response. A filter is said to be time or frequency stationary if its output is unaffected by the time or frequency of the input. A filter can also be classified as amplitude-only or phase-only depending on its response to the amplitude or phase of the input. Because a time stationary filter and a frequency stationary filter can be combined to make a linear filter with any arbitrary response, both are a necessary and sufficient requirement for the measurement of the electric field of an input pulse.
In a basic spectral shearing interferometer, the input beam is split into two identical pulses, sending one through a linear spectral phase modulator:
while the other is sent through a linear temporal phase modulator:
The two pulses are then recombined and sent through a spectrometer:
The linear spectral phase modulator is a time stationary, phase-only filter and adds spectral shear to pulses in its arm of the interferometer. The linear temporal phase modulator is frequency stationary, phase-only filter which adds temporal delay to the pulse in its arm. The spectrometer in which the pulses are recombined is a time stationary, amplitude-only filter which resolves with pass-band γ and center frequency ωc.
In this setup, the pulse through the temporal phase arm has its spectrum shifted by a spectral shear of Ω. In order to exactly measure a pulse, the field must be sampled by a certain number of spectrally sheared components. This sampling requirement is determined by the Nyquist–Shannon sampling theorem. If the function has compact support on the interval τN, then it is completely determined by giving its values at a series of frequencies 2π/τN apart. This means that the spectral shear that needs to be generated by the SPIDER is Ω = 2π/τN.
The pulse through the spectral arm acquires a time-delay of τ. The recombination of the pulses from the two arms is then resolved by the spectrometer which produces a signal
containing the spectrometer function, which can be approximated by a delta function due to its pass-band, γ, being so much narrower than the spectrum of the input pulse. In addition, because the spectral and temporal delays are fixed, the only remaining variable is the center frequency, ω_c, of the spectrometer. The resulting signal
contains the spectrum of the input pulse, the spectrum of the sheared pulse, and the phase difference between the frequency components of the input pulse which were separated by the spectral shear.
The shearing interferogram created by this signal generally consists of fringes spaced at a frequency of 2π/τ. Deviations from the nominal fringe spacing can be analyzed to obtain the spectral phase of the field. The spectral amplitude must be obtained by a separate measurement of the pulse spectrum.
Experimental set-up
The two arms in a spectral shearing interferometer are implemented by means of a beam splitter (B), Diffraction grating (G), lens (L), Aperture (A), Charge-coupled device C, and a method for sum frequency generation (S). These components make up the spectrometer and optical delay line.
Competing techniques
- Frequency-resolved optical gating
- Streak camera - not a significant competitor. Streak cameras have picosecond response times.
- Spatially Encoded Arrangement for SPIDER (For measuring few-cycle optical pulses.
- MIIPS Multiphoton Intrapulse Interference Phase Scan, a method to characterize and manipulate the ultrashort pulse.
See also
References
- Iaconis, C; Walmsley, I. A. (1999), "Self-Referencing Spectral Interferometry for Measuring Ultrashort Optical Pulses", IEEE J. Quantum Electron. 35 (4): 501–509, Bibcode 1999IJQE...35..501I, doi:10.1109/3.753654
- Iaconis, C; Walmsley, I. A. (1998), "Spectral Phase Interferometry for Direct Electric-Field Reconstruction of Ultrashort Optical Pulses", Opt. Lett. 23 (10): 792–794, Bibcode 1998OptL...23..792I, doi:10.1364/OL.23.000792, PMID 18087344, http://www.opticsinfobase.org/abstract.cfm?URI=ol-23-10-792
- Walmsley, I. A.; Wong, V. (1996), "Characterization of the Electric Field of Ultrashort Optical Pulses", J. Opt. Soc. Am. B 13 (11): 2453–2463, Bibcode 1996JOSAB..13.2453W, doi:10.1364/JOSAB.13.002453, http://www.opticsinfobase.org/abstract.cfm?URI=josab-13-11-2453
External links
- SPIDER page by Ian Walmsley (the inventor of SPIDER)
- new SPIDER page includes links to example code
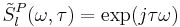
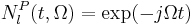
![\tilde{S}^A(\omega-\omega_c)=\exp \left [\frac{-(\omega-\omega_c)^2}{2\gamma^2} \right ]](/2012-wikipedia_en_all_nopic_01_2012/I/28480fd978af6558ba982eab7f5776b7.png)
![S(\omega_c;\Omega,\tau) = \int \left \{ \tilde{S}^A(\omega-\omega_c) \cdot \left [ \int N_l^P(\omega'-\omega) \tilde{E}(\omega)d\omega' %2B \tilde{S}_l^P(\omega) \tilde{E}(\omega) \right ] \right \}^2 d\omega](/2012-wikipedia_en_all_nopic_01_2012/I/25907e88f188c50a63651916c12bf1e7.png)
![S(\omega_c) = \left \{ \left | \tilde{E}(\omega_c - \Omega) \right |^2 %2B \left | \tilde{E}(\omega_c) \right |^2 %2B 2 \left | \tilde{E}(\omega_c-\Omega)\tilde{E}(\omega_c) \right |\cos \left [ \phi_{\omega}(\omega_c-\Omega)-\phi_{\omega}(\omega_c)-\tau\omega_c \right ] \right \}](/2012-wikipedia_en_all_nopic_01_2012/I/a61fcc28fe687f93ee597bad2f79b430.png)